Recent publications on gyroscopic effects describe the specificity of the action of inertial torques generated by the rotating mass of a spinning object. All inertial torques acting on the spinning object include resistance and precession torques generated by the external load. The external and inertial torques of the spinning object express their independent potential and kinetic energies, respectively, but the physics of their interaction needs to be clarified. The inertial torques and the motions of the gyroscope are based on the mechanical energy conservation law and presented by mathematical models about the axes of a Cartesian coordinate system. These motions arise from the combined action of a set of inertial torques produced by centrifugal and Coriolis forces, along with changes in angular momentum. Blocking of the gyroscope’s precessional motion nullifies all inertial torques except for the torque of the changes in angular momentum. The physics behind the selective nullification or deactivation of the inertial torques remains poorly understood. Identifying the reasons for the interrelated inertial torques’ nullification is a significant challenge for physicists. Addressing this issue within gyroscopic theory can simplify analytical solutions for various problems involving gyroscopic devices. This study describes the physics of inertial torque nullifications, offering valuable insights for researchers working on gyroscopic effects.
Gyroscopic effects have fascinated scientists since the Industrial Revolution [1, 2]. A significant contribution to the understanding of these effects was made by the mathematician L. Euler, whose theory of rigid body motion in 1765 introduced the concept of precession torque related to changes in angular momentum. This laid the groundwork for contemporary gyroscope theory [3, 4]. Many renowned scientists have studied gyroscopic phenomena, and their names are often mentioned in the history of gyroscope development [5]. Scientists from earlier centuries could not describe gyroscopic effects in principle, because the theory relies on several physical laws, the formulation of which was only completed at the beginning of the 20th century [6].
The simplified gyroscope theories proposed by several scientists have not been validated by practical applications [7]. The real gyroscope theory has more complex content than originally could imagine. Unresolved gyroscopic effects have been addressed through numerical modelling, which is still widely used in engineering [8]. In contemporary times, many papers discussing gyroscopic effects are published monthly, featuring mathematical models that aim to approximate the motions of gyroscopes [9]. However, these models overlook the conservation of kinetic energy in spinning objects, which is essential for understanding the dynamics of rotating bodies [10]. The existing gyroscope hypothesis is based on analytical calculations that focus solely on changes in angular momentum [11]. Unfortunately, these analytical models fail to compute gyroscopic effects and do not have practical applications in engineering [12]. The challenges associated with gyroscope problems relate to the mechanical energy conservation law. This is the reason that scientists of past centuries could not resolve all gyroscopic effects [13].
Most modern publications continue to examine gyroscopic effects related to gyroscope designs and data obtained from practical tests. Many studies highlight unresolved gyroscopic effects, prompting engineering industries to rely on costly numerical modelling for their applications [14, 15]. Textbooks on classical mechanics still describe gyroscopic effects based on Euler’s principle of angular momentum change, which does not provide a comprehensive solution [16, 17]. The theory of gyroscopes remains undeveloped, but upcoming presentations will offer elegant, straightforward, and rigorous mathematical models.
The intricate gyroscopic effects were a challenge for researchers who continually sought solutions. Recent studies on these effects have revealed that their underlying physics stems from the external load’s potential energy and the spinning rotor’s kinetic energy [18, 19]. The independent gyroscope’s potential and kinetic energies remain constant by the principle of mechanical energy conservation. Gyroscopic effects arise from the interaction of a set of inertial torques generated by centrifugal and Coriolis forces, and the torque resulting from changes in angular momentum [20, 21]. These effects are described around the axes of Cartesian coordinates and reflect the actions of resistance and precession inertial torques. The interplay between these two types of independent energies has been a challenge for physicists for over a century.
The published theory of gyroscopic effects for rotating objects establishes fundamental principles that explain the physics behind the properties of gyroscopic devices [20]. The method of cause-and-effect relationships has led to the development of accurate mathematical models for gyroscopic motion. The analytical models have been validated through practical tests. The motion of a gyroscope in space is described by equations of its rotation around the axes of Cartesian coordinates. Four inertial torques—generated by two centrifugal forces, one Coriolis force, and one change in angular momentum—act around each axis, resulting in the resistance and precession torques associated with gyroscopic effects. The interactions among these inertial torques express the angular velocities of the gyroscope’s rotation around its coordinated axes. The external load generates all inertial torques of the spinning object. In the absence of such load, the inertial torques are nullified. The external and inertial torques of the gyroscope express independent potential and kinetic energy, respectively. The blocking of the gyroscope’s precessional motion nullifies all inertial torques acting around one axis, except for the torques originating around the action of the load torque. This study provides a clear explanation of the physics involved in the nullification or deactivation of the resistance and precession torques.
The typical schema of the mathematical model for the motions of the spinning disc contains the external torque and demonstrates its motion at the accepted Cartesian coordinates [2– 5]. The action of the external torque around one axis on the spinning disc manifests its motions about two axes. Such dual motions of a spinning disc under the action of one external torque is the result of the action of interrelated inertial torques. The combined action of the torques manifests unusual reactions and motions of rotating objects in space that are called gyroscopic effects. This term is accepted in known publications that express the interrelated action of the torques and multi-axis motions of rotating objects.
The physics of the gyroscopic effects of the spinning disc should be considered in detail and thoroughly described [5, 6]. The reason for such a statement is motivated by the long-time absence of true mathematical models for the theory of gyroscopic effects in the known publications [7– 11]. Analysis of the action of the external torques on the spinning disc demonstrates the sequence chain of a generation of inertial torques and their actions around axes. The action of external and inertial torques on a spinning disc around two axes is strictly perpendicular to each other. This fact is explained by the spinning disc’s axis and its plane are strictly perpendicular to each other. The action of the interrelated torques is manifested by the big difference in the angular velocities around the axes of the spinning disc. The ratio of their angular velocities around axes is maintained and can be changed by the action of complex interdependency of the external and inertial torques on the spinning disc.
The action of the external and inertial torques around axes on the spinning disc is demonstrated in Figure 1, where the disc disposed symmetrically relatively of its supports at the system of Cartesian coordinate \(\Sigma xyz\). The interrelated action of the inertial torques is considered for the common case when the axis of the spinning disc turns in a counterclockwise direction about the axis \(ox\). The starting condition is considered the horizontal disposition of the spinning disc axis \(\gamma = 0\).
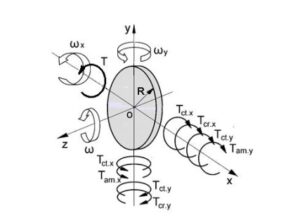
The following steps consider the action of the external torque \(T\) on the spinning disc that generates the sequential simultaneous activation of the inertial torques about two axes. The gyroscope motions about axes are implemented due to the interrelations of the inertial torques generated by the spinning disc [12, 16, 17].
The spinning disc rotates around axis \(oz\) with the angular velocity \(\omega\) illustrated by a circular tape arrow in the counter-clockwise direction. The spinning disc turns down in the counterclockwise direction about axis \(ox\) with the angular velocity \(\omega_x\) (illustrated by a circular tape arrow) under the action of the external load torque \(T\) (illustrated by a circular bold arrow);
At the starting condition, the external torque \(T\) produces the initial resistance torques (\(T_{ct.x}\) and \(T_{cr.x}\) illustrated by circular thin arrows) that are generated by the centrifugal (index \(ct\)) and Coriolis (index \(cr\)) forces, which are resistance torques acting about axis \(ox\), and contradict the action of the external torque \(T\).
The initial resistance torques (\(T_{ct.x}\) and \(T_{cr.x}\)) act in the clockwise direction, i.e., opposite to the action of the external torque \(T\) but the turn of the spinning disc is in the direction of the action of the external torque \(T\).
At the starting condition, the external torque \(T\) generates the initial precession torques (\(T_{ct.x}\) and \(T_{am.x}\) illustrated by circular thin arrows) that are produced by the centrifugal forces and the change in the angular momentum (index \(am\)). These two initial precession torques are load torques for the spinning disc and originate along with axis \(ox\) but act about axis \(oy\) in the counter-clockwise direction. The initial resistance (\(T_{ct.x}\) and \(T_{cr.x}\)) and precession (\(T_{ct.x}\) and \(T_{am.x}\)) torques are acting about axes \(ox\) and \(oy\) respectively and simultaneously. The equations of their inertial torques comprise one angular velocity \(\omega_x\) about axis \(ox\).
The spinning disc turns in the counter-clockwise direction about axis \(oy\) under the action of the initial precession torques (\(T_{ct.x}\) and \(T_{am.x}\)):
The initial precession torques (\(T_{ct.x}\) and \(T_{am.x}\)) acting about axis \(oy\) in the counterclockwise direction generate the resistance torques (\(T_{ct.y}\) and \(T_{cr.y}\) illustrated by circular thin arrows) of centrifugal and Coriolis forces acting about axis \(oy\), which act in a clockwise direction.
The resulting torque, which is the combination of the initial precession (\(T_{ct.x}\) and \(T_{am.x}\)) and resistance (\(T_{ct.y}\) and \(T_{cr.y}\)) torques, acts about axis \(oy\) and rotates the spinning disc with the angular velocity \(\omega_y\) (illustrated by a circular tape arrow). This resulting torque \[T_{r.y} = T_{ct.x} + T_{am.x} – T_{ct.y} – T_{cr.y},\] generates the precession torques (\(T_{ct.y}\) and \(T_{am.y}\)) of centrifugal forces and the change in the angular momentum acting about axis \(ox\). The precession torques (\(T_{ct.y}\) and \(T_{am.y}\)) act opposite to the direction of the external torque \(T\). The sum of the initial resistance torques (\(T_{ct.x}\) and \(T_{cr.x}\)) and the precession torques (\(T_{in.y}\) and \(T_{am.y}\)) constitutes the resulting resistance torque \(\Sigma T_{r.x} = T_{ct.x} + T_{cr.x} + T_{ct.y} + T_{am.y}\) acting opposite to the direction of the external torque \(T\). The centrifugal torques \(T_{ct.y}\) acting around axes \(oy\) and \(ox\) are subtracted and do not act on the other torques. The resulting torque \(T_y\) acting around the axis \(oy\) acts as the precession torque \(T_{am.y}\) around the axis \(ox\).
The total resulting torque acting about axis \(ox\) is represented by the following equation \[T_x = T – \Sigma T_{r.x} = T – (T_{ct.x} + T_{cr.x} + T_{ct.y} + T_{am.y}).\]
The total resulting torque acting about axis \(ox\), \(T_x\), represents the combined external and inertial torques that generate the precession torques acting about axis \(oy\) (\(T^*_{ct.x}\) and \(T^*_{am.x}\)) that is not the same as initial at starting condition (paragraph 1). The precession torques (\(T^*_{ct.x}\) and \(T^*_{am.x}\)) in turn generate the resistance torque (\(T^*_{ct.y}\) and \(T^*_{cr.y}\)). The total resulting torque acting about axis \(oy\) is presented by the following equation
\[T_y = T^*_{ct.x} + T^*_{am.x} – (T^*_{ct.y} + T^*_{cr.y}).\]
The chain of the sequencing and simultaneous action of the inertial torques generated by the one external torque looped about two axes demonstrates their cause-and-effect relationships and explains their physics. The system of interrelated inertial torques cannot be separated from the action of the individual or a group of external torques. All inertial torques are generated by one rotating mass of the spinning disc. A described peculiarity of the action of gyroscopic torques on the spinning disc expresses clearly the physics of their origination that is manifested by gyroscopic motions around axes. The action of the external torque about two axes and the interrelation with the inertial torques can be formulated by two mathematical equations [12, 16, 17, 22, 23].
Practically, gyroscopic devices can operate under different conditions of the action of the external torques and the angular velocities of the gyroscope around axes. The action of the several external torques will generate their system and values of the inertial torques of spinning objects. Due to the interrelations of the external and inertial torques acting on spinning objects, any change in values of inertial torques originating along one axis will lead to a change in values of inertial torques acting about another axis and vice versa. This statement follows up on the interrelations of the gyroscopic torques described above.
Analysis of the actions of the external and inertial torques about two axes shows the following:
The inertial torques acting about axis \(ox\) contain the looped resistance and precession inertial torques generated by the centrifugal, and Coriolis forces as well as the change in the angular momentum (\(T_{ct.x}\), \(T_{cr.x}\), \(T_{ct.y}\), and \(T_{am.y}\)).
The inertial torques acting about axis \(oy\) contain the resistance and precession inertial torques generated by the same inertial forces (\(T_{ct.y}\), \(T_{cr.y}\), \(T_{ct.x}\), and \(T_{am.x}\)).
The inertial torques acting about each axis contain one set of resistance and precession inertial torques. These inertial torques express mechanical energies generated by the potential energy of the external torque and kinetic energy of the spinning disc. The kinetic energies of the inertial torques acting about axes are distributed equally along axes \(ox\) and \(oy\) due to their interrelations.
The value of the inertial torques, angular velocities, and their interrelations with the axes of the spinning disc is maintained by the principle of the mechanical energy conservation law.
The external load torque generates the resistance and precession inertial torques which are the internal torques acting about two axes. The action of the resulting precession torques around axes is looped with feedback by the principle of kinetic energy conservation.
Mathematical models for the inertial torques generated by the external load acting on the rotating disc are represented in Table 1 [20] which constitute fundamental principles of the theory of gyroscopic effects.
| The basis of the theory of gyroscopic effects is the mechanical energy conservation law | ||
| 1. Inertial torques acting on the theory of gyroscopic effects about axis \(i\) | ||
| Type of the torque generated by | Action | Equation |
| Centrifugal forces | Resistance | \(T_{ct.i} = \frac{4}{9} \pi^2 J \omega \omega_i\) |
| Precession | ||
| Coriolis forces | Resistance | \(T_{cr.i} = \frac{8}{9} J \omega \omega_i\) |
| Change in angular momentum | Precession | \(T_{am.i} = J \omega \omega_i\) |
| 2. The dependency of angular velocities of the spinning disc about axes | ||
| \(\omega_j = – (8\pi^2 + 17)\, \omega_i\) | ||
|
\(J\) is the disc moment of inertia and \(\omega\) is its angular velocity;
\(\omega_i\) is the angular velocity of the disc about axis \(i\). |
||
The expressions for the inertial torques generated by the rotating mass of the spinning disc show all of them contain the major component which is the change in the angular momentum (Table 1). The numerical coefficients of the inertial toques and the ratio of the angular velocities for the rotation of the spinning disc express the origins of inertial toques that depend on the geometry of the spinning objects.
The inertial torques generated by the rotating masses of the spinning rotor (Table 1) are presented by the expression \(T_i = D_i J \omega \omega_x\) where \(D_i\) is the factor that depends on the type of torque, i.e., generated by the centrifugal, Coriolis, and the change in the angular momentum; \(J\) is the moment of inertia of the spinning rotor, \(\omega\) is the angular velocity of the rotor; \(\omega_x\) is the angular velocity of the rotor around axis \(ox\) [20]. The expression \(T_i\) comprises two components \(\omega\) and \(\omega_i\) which the product \(\omega \omega_i = \varepsilon_i\) is the acceleration about axis \(i\). The running gyroscope under the action of the external torques rotates with the angular velocities \(\omega_x\), \(\omega_y\), and \(\omega\) about axes \(ox\), \(oy\), and \(oz\), respectively. The load torque acting around the axes \(ox\) and \(oy\) generates the resistance and precession torques acting around axes \(ox\), \(oy\), and \(oy\), \(ox\), respectively. The expression of the resulting inertial torques acting on the spinning rotor around the axes \(ox\) and \(oy\) are
\[T_x = \frac{4\pi^2}{9} J \omega \omega_x + \frac{8}{9} J \omega \omega_x + \frac{4\pi^2}{9} J \omega \omega_y + J \omega \omega_y,\] and \[T_y = \frac{4\pi^2}{9} J \omega \omega_x + J \omega \omega_x – \frac{4\pi^2}{9} J \omega \omega_y – \frac{8}{9} J \omega \omega_y,\] respectively [20]. The expressions of their inertial torques comprise the components of accelerations \(\omega \omega_x = \varepsilon_y\) and \(\omega \omega_y = \varepsilon_x\) of the gyroscope about axes \(oy\) and \(ox\), respectively. The action of all inertial torques about axes is kinetically interrelated. The blocking of the turn of the running gyroscope about any axis causes its rotation about axes to stop because of the accelerations \(\varepsilon_y = 0\) and \(\varepsilon_x = 0\) and the absence of the angular velocities \(\omega_x = 0\) and \(\omega_y = 0\). The variable angular velocities of the gyroscope about axis \(ox\) and \(oy\) as the result of the simultaneous action of the gyroscope weight and inertial torques generated by the spinning rotor. All inertial torques (Figure 1) have the zero values \(T_i = 0\), i.e., nullified or they are deactivated at the condition of blocking the gyroscope motion around axes of rotation. At this condition, the angular velocity of the spinning rotor \(\omega\) is constant, and a gyroscope turns down under the action of the gyroscope weight and frictional forces acting on the supports. The running gyroscope moves with the gravity acceleration when its motion about the axis \(oy\) is blocked which was confirmed by the practical tests.
The vectorial diagram of the angular velocities and accelerations of the spinning rotor about axes are presented in Figure 2. All rotational motions of the gyroscope about axes are in the counter-clockwise directions if considered from the tips of the coordinate axes.
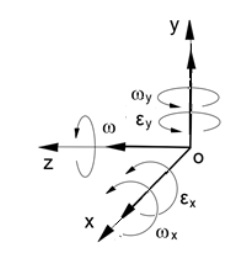
The inertial torques of the centrifugal and Coriolis forces and the torque of the change in the angular momentum generated by rotating mass about axes ox and oy are expressed indirectly in the kinetic energies of the gyroscope motions and spinning rotor. The nullification or deactivation of the inertial torques is going on for quite a short time. Practical tests [20] show this process depends on the values of the external torques, the mass moment of inertia, J, the angular velocity of the spinning rotor \(\omega\), and the angular velocity of the gyroscope rotation about axes \(\omega_i\). Blocking of rotation of the running gyroscope around axis oy is manifested by the nullification of the values of the inertial torques generated by the rotating mass of the spinning disc and a gyroscope turns down faster with gravity acceleration. This free motion of the running gyroscope is the same as for the pendulum twisting and does not contradict the laws of physics. The conducted analysis elucidates the nullification of the gyroscopic inertial torques as one gyroscopic effect. The following properties of gyroscopic effects underline their interrelation with independent energies of the external torque and the spinning rotor.
The potential energy of the external torque \(T\) and the kinetic energy of the spinning disc are converted into kinetic energies of the resistance and precession torques with the disc angular velocities of \(\omega_x\) and \(\omega_y\), around two axes \(ox\) and \(oy\) at the Cartesian coordinates (Figure 1 and Table 1) [20].
The increase of the angular velocity \(\omega\) of the spinning disc leads to the right increase in the values of the inertial torques \(T_i\) and to a decrease in the angular velocities of the disc \(\omega_x\) and \(\omega_y\).
The inertial torques cannot be separated because they are generated by one rotating mass of the spinning disc and interrelated with looped feedback.
Blocking of the motion of the spinning disc about the axis \(ox\) or absence of the external torque \(T\) nullifies all inertial torques (Table 1) and the angular velocities about two axes, which is obvious (Figure 1) by the principle of classical mechanics.
Blocking of the motion of the spinning disc about the axis \(oy\), (the external torque \(T\) is acting), nullifies all inertial torques (Table 1) and the angular velocities \(\omega_x\) and \(\omega_y\) about two axes. The spinning disc rotates around axis \(ox\) with a high angular velocity under the action only of the external torque \(T\) which generates the single torque of the change in the angular momentum acting around the axis \(oy\). This condition and action of the single inertial torque also represent the gyroscopic effect which physics are described by the following properties:
The kinetic energies of the disc rotation around the axes \(oy\) and \(ox\) are nullified because: the angular velocity, \(\omega_y = 0\), hence, \(\omega \omega_x = \varepsilon_y = 0\), from this \(\omega_x = 0\) and acceleration \(\varepsilon_x = 0\), because \(\omega \omega_y = \varepsilon_x = 0\). From this it follows that all inertial torques originated along the axes \(oy\) and \(ox\) are nullified because interrupted the looped feedback circuit of inertial torques.
The interrelation of potential energy of the external torque \(T\) and kinetic energy of the spinning disc receives new dependency. The new angular velocity \(\omega_x^* \neq 0\) of the disc rotation around the axis \(ox\) manifests the action of the external torque \(T\) (potential energy) and the angular momentum of the spinning disc (kinetic energy) that generate the torque of the change in the angular momentum \(T_{am.x} = J \omega \omega_x^*\) acting around axis \(oy\) (Figure 1). This fact is validated by the practical tests [20]. Additionally, the angular velocity \(\omega_x^* \gg \omega_x\) because no resisting inertial torques are acting on the spinning disc around the axis \(ox\).
The inertial torques’ action on the spinning disc and its stopping of motions around the axes described above explain the physics of inertial torque nullification or deactivation. The spinning disc inertial torques differ from the inertial torque of the simple pendulum. The practical observation of motions of the gyroscope and analytical study demonstrated the manifestation form of its mechanical energies.
The physics of gyroscopic effects became understandable by stepped analysis of the action of external torques generated by the inertial torques of the spinning disc around the axes of the Cartesian coordinates. The interrelated dependency of inertial torques was discovered by the method of cause and effect relationship and showed their looped and feedback circuit. The interrelated inertial toques of feedback express the equality of kinetic energies of the spinning disc about axes of rotation. The inertial toques and the dependency of rotations of the spinning disc around axes constitute the fundamental principles of the theory of gyroscope effects for rotating objects based on the mechanical energy conservation law. The action of the external torque expresses the potential energy of the gyroscope that is converted to the kinetic energy of the gyroscope rotation around axes and the action of inertial torques. The blocking of the external torque acting on the running gyroscope yields nullification of its kinetic energies around two axes. The blocking of the precessed motion of the running gyroscope around one axis yields a change in its kinetic energy around one axis. The resulting torques acting around two axes are equal by the principle of the equality of the kinetic energies around two axes that are maintained by a closed feedback loop system. The gyroscope rotates around one axis oy with new angular acceleration. The action of all gyroscopic torques around axes is maintained by the mechanical energy conservation law that is validated by the practical test. The two types of kinetic energies of the gyroscope are expressed by the system of the action of the set of inertial torques and motions around axes. The action of the interrelated inertial torques and the gyroscopic motions enable an understanding of the physics of gyroscopic effects.
The fundamental laws of classical mechanics were finalized at the beginning of the last century, allowing physicists to solve many problems related to gyroscopic effects in rotating objects. However, until recently, these issues remained unsolvable. To address this in engineering applications, expensive numerical models were used for various gyroscopic devices. Recent studies in the physics of rotating bodies have uncovered the fundamental principles of gyroscopic effects, which are described by mathematical models of classical mechanics. This theory is now being used in practical applications, and new research indicates that a spinning object in space experiences twelve inertial torques when subjected to a single external torque. The methods derived from gyroscope theory allow for manual computation of gyroscopic effects for rotating objects of different designs in engineering. The physics of inertial torques acting on spinning objects and their nullifications is well described by the fundamental principles of classical mechanics. Artificial terms such as the gyroscope antigravity effect, gyroscope couple, gyroscope resistance, non-inertial gyroscope, etc., previously coined by researchers, have been removed from the glossary of gyroscope theory. The application of the fundamental principles of gyroscopic effects enables the formulation of mathematical models for problems off gyroscopic devices.
The Kyrgyz State Technical University after I. Razzakov supported the research work for a publication that was performed as part of the employment. The author did not receive specific funding support for the article and does not have any potential conflict of interest.
The author declares that the data supporting the findings of this study are available within the paper with references.
The author declares that he has no conflicts of interest.
The author declares that this research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
Irato, G. (2015). On the historical evolution of gyroscopic instrumentation: a very brief account. HAL Id: Hal-01136829, https://hal.archives-ouvertes.fr/hal-01136829.
Range, S. K., & Mullins, J. (2011). Brief History of Gyroscopes.
Greenhill, G. (2015). Report on Gyroscopic Theory. Relink Books, Fallbrook, CA, USA.
Scarborough, J. B. (2011). The Gyroscope Theory and Applications. Nabu Press, London.
Deimel, R. F. (2003). Mechanics of the Gyroscope. Dover Publications Inc., New York.
Awrejcewicz, J., & Koruba, Z. (2012). Classical Mechanics: Applied Mechanics and Mechatronics (Vol. 30). Springer Science & Business Media.
Turner, G. (2007). Gyroscopes. Brightfusion Ltd, London, 1st edition.
Klein, F., & Sommerfeld, A. (2008). The Theory of the Top. Volume I: Introduction to the Kinematics and Kinetics of the Top (Vol. 1). Springer Science & Business Media.
Passaro, V. M., Cuccovillo, A., Vaiani, L., De Carlo, M., & Campanella, C. E. (2017). Gyroscope technology and applications: A review in the industrial perspective. Sensors, 17(10), 2284.
Peshekhonov, V. G. (2020). The outlook for gyroscopy. Gyroscope and Navigation, 11(2), 193–197.
Cordeiro, F. J. B. (2018). The Gyroscope. FB&C Limited.
Hibbeler, R. C. (2010). Engineering Mechanics – Statics, and Dynamics. Prentice-Hall, Pearson, Singapore, 12th edition.
Guran, A., Ishida, Y., & Bajaj, A. (1999). Dynamics Gyroscopic Systems. World Scientific Publishing Company.
Armenise, M. N., Ciminelli, C., Dell’Olio, F., & Passaro, V. M. (2010). Advances in Gyroscope Technologies. Springer Science & Business Media.
Zhuang, X., & Zhou, L. (2020). Gyroscopes: Principles and Applications. IntechOpen.
Germain, P., Piau, M., & Caillerie, D. (2012). Theoretical and Applied Mechanics. Elsevier.
Gregory. D. R. (2006). Classical Mechanics. Cambridge University Press, New York.
Crassidis, J. L., & Markley, F. L. (2016). Three-axis attitude estimation using rate-integrating gyroscopes. Journal of Guidance, Control, and Dynamics, 39(7), 1513-1526.
Liang, W. C., & Lee, S. C. (2013). Vorticity, gyroscopic precession, and spin-curvature force. Physical Review D—Particles, Fields, Gravitation, and Cosmology, 87(4), 044024.
Usubamatov, R. (2020). Theory of Gyroscopic Effects for Rotating Objects. Springer, Cham, Switzerland, 2nd edition.
Usubamatov, R., & Allen, D. (2022). Corrected inertial torques of gyroscopic effects. Advances in Mathematical Physics, 2022(1), 3479736.
Ardema, M. D. (2005). Analytical Dynamics: Theory and Applications. Springer Science & Business Media.
Taylor, J. R. (2005). Classical Mechanics. University science book.