Existence, Stability and Instability conditions of a Static Meniscus Appearing in Tube Single Crystal Growth from Melt using E.F.G. Method

1. Introduction

The growth of silicon tubes by the edge-defined film-fed growth (E.F.G.) process was first reported by Erris et al. [1]. In [1] a theory of tube growth by the E.F.G. process is developed to show the dependence of tube wall thickness on the growth variables. The theory uses approximations reported in [2, 3], and it has been shown to be a useful tool for understanding the feasible limits of wall-thickness control. A more accurate predictive model would require an increase of the acceptable tolerance range introduced by approximation. Later, the heat flow in a tube growth system was analyzed in [4– 13]. The state of the art at the time 1993–1994, concerning the calculation of the meniscus shape in general in the case of growth by the E.F.G. method, is summarized in [14]. According to [14], for the general differential equation describing the free surface of a liquid meniscus, possessing axial symmetry, there is no complete analysis and solution. For the general equation only numerical integrations were carried out for a number of process parameter values that were of practical interest at the moment. The authors of [15, 16] consider automated crystal growth processes based on weight sensors and computers. They give an expression for the weight of the meniscus, contacted with crystal and shaper of arbitrary shape, in which there are two terms related to the hydrodynamic factor. In [17] it is shown that the hydrodynamic factor is too small to be considered in automated crystal growth. In [18] a theoretical and numerical study of meniscus dynamics, under symmetric and asymmetric configurations, is presented. A meniscus-dynamics model is developed to consider meniscus shape and its dynamics, heat and mass transfer around the die top and meniscus. Analysis reveals the correlations among tube thickness, effective melt height, pull rate, die-top temperature, and crystal environmental temperature. In [19] the effect of the controllable part of the pressure difference on the free-surface shape of the static meniscus is analyzed for the tube growth by the E.F.G. method for materials for which \(0<\alpha_c<\pi/2\), \(0<\alpha_g<\pi/2\), and \(\alpha_c>\pi/2-\alpha_g\), and in [20] a similar analysis is presented for materials for which \(\pi/2>\alpha_c>\pi/2-\alpha_g\).

Tube-shaped single crystals are finding applications in medical devices due to their unique properties. Specifically, they are used in ultrasonic transducers, where their piezoelectric properties enable high-frequency imaging and therapy. These crystals, often made of materials like PMN–PT or PIN–PMN–PT, offer superior performance compared to traditional materials, leading to advancements in medical imaging and diagnostics. Tube-shaped single crystals, like YAG:Ce single crystals, are used as scintillators in radiation imaging sensors, producing high-quality images. PMN–PT single crystals, known for their piezoelectric properties, are used in ultrasonic transducers for both diagnostic and therapeutic ultrasound applications. These crystals can be fabricated into phased arrays for 3D and 4D imaging, offering enhanced imaging capabilities.

The imaging and surgical ecosystem considered here spans illumination, access, therapy, and diagnostics. A robust YAG:Ce single crystal light source enables ultra-high-efficiency illumination for minimally invasive optics (Fig. 1), which integrates with the endoscope–camera–video chain and the laparoscope for in-body visualization (Figs. 5 and 6). On the therapeutic side, ultrasonic vessel sealing and dissection support precise hemostasis in soft-tissue surgery (Fig. 2), while 3D ultrasound approaches are being explored for treating neurological diseases (Fig. 3). For diagnostic imaging fundamentals, a representative linear-array scan demonstrates beamforming and resolution trade-offs (Fig. 4), and two clinical-grade platforms—the Ecograf Acuson Origin and the Ecograf Acuson Sequoia—illustrate modern system implementations across workflows (Figs. 7 and 8).

This study presents necessary conditions for the existence and sufficient conditions for the stability or instability of the static menisci (liquid bridges) appearing in the single-crystal tube growth from the melt, of predetermined sizes, by using the edge-defined film-fed (E.F.G.) growth method. The results are significant for single-crystal tube growth from melt, with prior given macroscopic dimensions, using prior given specific equipment.

2. The free surfaces equations and the pressure differences

At the beginning is important to note is that in case of tube the meniscus has two free surfaces one inner free surface and one outer free surface. The free surfaces of the static meniscus, in single crystal growth by EFG method, in hydrostatic approximation are described by the Young-Laplace capillary equation [21]: \[\begin{aligned} \label{eq2.1}\begin{cases} \gamma\!\left(\frac{1}{R_{1i}}+\frac{1}{R_{2i}}\right)=&P_{ai}-P_{mi}, \\ \gamma\!\left(\frac{1}{R_{1e}}+\frac{1}{R_{2e}}\right)=&P_{ae}-P_{me}, \end{cases} \end{aligned} \tag{1}\] here, \(\gamma\) is the melt surface tension; \(\frac{1}{R_{1i}},\frac{1}{R_{2i}}\) denote the main normal curvatures of the meridian arc of the inner free surface and \(\frac{1}{R_{1e}},\frac{1}{R_{2e}}\) denote the main normal curvatures of the meridian arc of the outer free surface; \(P_{ai}\) and \(P_{ae}\) is the pressure above the inner and the outer free surface respectively, equal to the pressure of the gas flow introduced in the tube and in the furnace respectively [21], denoted by \(p_{gi}\) \(\left(P_{ai}=p_{gi}\right)\) and \(p_{ge}\) \(\left(P_{ae}=p_{ge}\right)\). The pressures \(P_{mi}\) and \(P_{me}\) under the inner and the outer free surface respectively are equal to \(-\rho g\,(z_i+H)\) and \(-\rho g\,(z_e+H)\) respectively (the direction of \(Oz\) is upwards, see Figures 9 and 10). \(\rho\) denotes the density of the melt and \(g\) the gravity acceleration; \(H\) denotes the height difference between the top of the shapers and the melt level in crucible\(\,\)—\(\,\)the distance between the shapers top level and the crucible melt level. \(H\) is positive when the crucible melt level is under the shapers top level and it is negative when the shapers top level is under the crucible melt level (see Figures 9 and 10). The meridian curve of the inner free surface of meniscus is denoted by \(z_i(r)\) and that of the outer free surface is denoted by \(z_e(r)\) (see Figures 9 and 10).

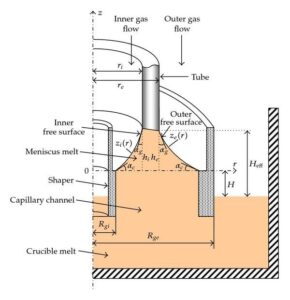
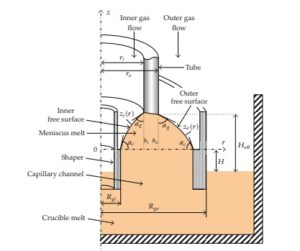
In hydrostatic approximation the Young–Laplace capillary surface equations (1) can be written as: \[\begin{aligned} \label{eq2.2}\begin{cases} \gamma\!\left(\frac{1}{R_{1i}}+\frac{1}{R_{2i}}\right)=&\rho g\,z_i-p_i,\\ \gamma\!\left(\frac{1}{R_{1e}}+\frac{1}{R_{2e}}\right)=&\rho g\,z_e-p_e,\end{cases} \end{aligned} \tag{2}\] respectively, where \[\begin{aligned} \label{eq2.3}\begin{cases} p_i=&-\,p_{gi}-\rho g\,H\,,\\ p_e=&-\,p_{ge}-\rho g\,H\,,\end{cases} \end{aligned} \tag{3}\] respectively.

To calculate the meniscus surface shape and size in hydrostatic approximation is convenient to express the Young–Laplace Eqs. (2) in differential form with respect to an axisymmetric reference frame (see Figure 9 and Figure 10) in terms of the meridian curves \(z_i(r)\) and \(z_e(r)\) respectively. According to [20, 21] these equations in terms of the inner and outer meridian curves are: \[\label{eq2.4} z_i''=\frac{\rho g\,z_i-p_i}{\gamma}\,\bigl[1+(z_i')^2\bigr]^{\frac{3}{2}} -\frac{1}{r}\,\bigl[1+(z_i')^2\bigr]\,z_i', \quad \text{for } \quad 0< R_{gi}\le r\le r_i, \tag{4}\] where \(r_i>0\) is the single crystal tube inner radius and \(R_{gi}\) (\(R_{gi}>r_i\)) is the shaper inner radius, \[\label{eq2.5} z_e''=\frac{\rho g\,z_e-p_e}{\gamma}\,\bigl[1+(z_e')^2\bigr]^{\frac{3}{2}} -\frac{1}{r}\,\bigl[1+(z_e')^2\bigr]\,z_e', \quad \text{for }\quad 0< r_e< r< R_{ge}, \tag{5}\] where \(r_e>0\) is the single crystal tube outer radius and \(R_{ge}\) (\(r_e<R_{ge}\)) is the shaper outer radius. It is assumed that the above radii verify: \(R_{gi}<r_i<r_e<R_{ge}\).

Remark that the Young–Laplace capillary Eqs. (4), (5) are the Euler equations of the free energy of the inner and outer melt columns respectively, i.e. they are the first order necessary conditions of minimum of functional \(I_i(z)\) and \(I_e(z)\) defined by: \[\label{eq2.6} I_i(z_i)=\int_{R_{gi}}^{\,r_i}\!\left\{\gamma\sqrt{1+(z_i')^2} +\frac{1}{2}\rho g\,z_i^2-p_i z_i\right\} r\,dr,\qquad z_i(r_i)=h_i,\; z_i(R_{gi})=0, \tag{6}\] \[\label{eq2.7} I_e(z_e)=\int_{r_e}^{\,R_{ge}}\!\left\{\gamma\sqrt{1+(z_e')^2} +\frac{1}{2}\rho g\,z_e^2-p_e z_e\right\} r\,dr,\qquad z_e(r_e)=h_e,\; z_e(R_{ge})=0, \tag{7}\] respectively. This means that the Young–Laplace Eqs. (4), (5) can be obtained starting from the general Euler equations: \[\label{eq2.8} \frac{d}{dr}\!\left(\frac{\partial F_i}{\partial z_i'}\right)-\frac{\partial F_i}{\partial z_i}=0, \qquad \frac{d}{dr}\!\left(\frac{\partial F_e}{\partial z_e'}\right)-\frac{\partial F_e}{\partial z_e}=0, \tag{8}\] which are the first order necessary conditions of minimum of the functionals, \(I_i(z_i)\), \(I_e(z_e)\), and taking \[\label{eq2.9} F_i(r,z_i,z_i')=\left\{\gamma\sqrt{1+(z_i')^2}+\frac{1}{2}\rho g\,z_i^2-p_i z_i\right\} r, \tag{9}\] \[\label{eq2.10} F_e(r,z_e,z_e')=\left\{\gamma\sqrt{1+(z_e')^2}+\frac{1}{2}\rho g\,z_e^2-p_e z_e\right\} r. \tag{10}\]

As the Young–Laplace equations in hydrostatic approximation (4) and (5) are second order ordinary differential equations, formulation of boundary conditions requires assignment of two boundary conditions; one of the melt crystal interface, the second one on the melt and shaper interface. These conditions are: \[\label{eq2.11} z_i'(R_{gi})=\tan(\alpha_c),\qquad z_i'(r_i)=\tan\!\left(\frac{\pi}{2}-\alpha_g\right),\qquad z_i(R_{gi})=0,\qquad z_i(r_i)=h_i, \tag{11}\] where \(\alpha_g\) is the growth angle, \(\alpha_c\) is the contact angle between the meniscus free surface and the edge of the inner shaper top and \(h_i\) is the height of the meniscus inner surface; and \[\label{eq2.12} z_e'(R_{ge})=-\tan(\alpha_c),\qquad z_e'(r_e)=-\tan\!\left(\frac{\pi}{2}-\alpha_g\right),\qquad z_e(R_{ge})=0,\qquad z_e(r_e)=h_e, \tag{12}\] where \(h_e\) is the height of the meniscus outer surface.

3. Existence, Stability or Instability of a meniscus having convex inner and outer free surface

The inner and outer free surface of a meniscus is convex if \(z_i''(r)>0\) and \(z_e''(r)>0\) for \(R_{gi} \le r \le r_i\) and \(r_e < R_{ge}\), respectively.

Remark first that in case of a meniscus having convex inner and outer surfaces the functions \(z_i'(r)\), \(z_e'(r)\) are increasing. For the inner meridian curve this means that the angle between the tangent line to the inner curve \(z_i(r)\), in every point \(r\), and the \(Or\) axis, \(\alpha_i(r)=\arctan z_i'(r)\), is increasing. In particular, it follows that \(\alpha_i(R_{gi})<\alpha_i(r_i)\). Since \(\alpha_i(R_{gi})=\alpha_i\) and \(\alpha_i(r_i)=\frac{\pi}{2}-\alpha_g\), we obtain inequality \(\frac{\pi}{2}-\alpha_g > \alpha_i\), or \(\alpha_g > \alpha_c >0\). (see Figure 9).

For the outer surface meridian curve convexity means that the angle between the tangent line to the meridian curve \(z_e(r)\), in every point \(r\), and the \(Or\) axis, \(\alpha_e(r)=-\arctan z_e'(r)\), is decreasing. In particular, it follows that \(\alpha_e(R_{ge})<\alpha_e(r_e)\). Since \(\alpha_e(R_{ge})=\alpha_e\) and \(\alpha_e(r_e)=\frac{\pi}{2}-\alpha_g\), we obtain inequality \(\frac{\pi}{2}-\alpha_g > \alpha_e\), or \(\alpha_g > \alpha_c >0\) (see Figure 9). Therefore if the inner and outer free surface of a meniscus is convex then \(\frac{\pi}{2}-\alpha_g > \alpha_c\).

Using the Young-Laplace capillarity Eqs. (4) and (5) and conditions (11) and (12) respectively in [20] the following result was established:

If \(p_i\) and \(p_e\) there exists a solution \(z_i(r)\) of Eq. (4) and a solution \(z_e(r)\) of Eq. (5) respectively, which are convex meridian curves and describes the inner and outer free surfaces of a static meniscus respectively, then the following inequalities hold: \[\begin{aligned} \label{eq3.1} -\gamma &\frac{\pi}{X} \frac{(a_g+\alpha_c)}{R_{gi}} \cos \alpha_c – \frac{Y}{R_{gi}} \sin \alpha_c\notag\\ &\le p_i \le -\gamma \frac{\pi}{X} \frac{(a_g+\alpha_c)}{r_i – R_{gi}} \sin \alpha_g + (r_i – R_{gi}) \times \rho \times g \times X \tan\left(\frac{\pi}{2}-\alpha_g\right) = \frac{Y}{X} \sin \alpha_c, \end{aligned} \tag{13}\] \[\begin{aligned} \label{eq3.2} -\gamma &\frac{\pi}{X} \frac{(a_g+\alpha_c)}{R_{ge}} \cos \alpha_c + \frac{Y}{R_{ge}} \sin \alpha_c \notag\\&\le p_e \le -\gamma \frac{\pi}{X} \frac{(a_g+\alpha_c)}{R_{ge}-r_e} \sin \alpha_g + (R_{ge}-r_e) \times \rho \times g \times X \tan\left(\frac{\pi}{2}-\alpha_g\right) = \frac{Y}{X} \cos \alpha_g. \end{aligned} \tag{14}\]

Therefore in case of the existence of a computed static meniscus for which the inner and outer surfaces are convex then the values of the pressure differences \(p_i = -p_{gi} – \rho \times g \times H\) and \(p_e = -p_{ge} – \rho \times g \times H\) has to be in the interval \(\left[L_i^{left}, L_i^{right}\right]\) and \(\left[L_e^{left}, L_e^{right}\right]\) respectively where:

\[ L_i^{left} = -\gamma \times \frac{\pi}{X} \frac{(a_c + a_g)}{r_i – R_{gi}} \times \cos \alpha_c – \frac{Y}{R_{gi}} \times \cos \alpha_g,\label{eq3.3}\ \tag{15}\] \[ L_i^{right} = -\gamma \times \frac{\pi}{X} \frac{(a_c + a_g)}{r_i – R_{gi}} \times \sin \alpha_g + (r_i – R_{gi}) \times \rho \times g \times \tan \left( \frac{\pi}{2} – \alpha_g \right) – \frac{Y}{r_i} \sin \alpha_c, \label{eq3.4}\ \tag{16}\] \[ L_e^{left} = -\gamma \times \frac{\pi}{X} \frac{(a_c + a_g)}{R_{ge} – r_e} \times \cos \alpha_c + \frac{Y}{R_{ge}} \times \sin \alpha_c,\label{eq3.5}\ \tag{17}\] \[ L_e^{right} = -\gamma \times \frac{\pi}{X} \frac{(a_c + a_g)}{R_{ge} – r_e} \times \sin \alpha_g + (R_{ge} – r_e) \times \rho \times g \times \tan \left( \frac{\pi}{2} – \alpha_g \right) + \frac{Y}{r_e} \cos \alpha_g.\label{eq3.6} \tag{18}\]

For the practical existence of a static meniscus having the inner and outer free surfaces convex numerical computations were performed for Si thin tube growth using the following numerical data: \(R_{gi} = 4.2 \times 10^{-3}\,[m], \, r_i = 4.35 \times 10^{-3}\,[m], \, R_{ge} = 4.8 \times 10^{-3}\,[m], \, r_e = 4.65 \times 10^{-3}\,[m], \, \alpha_c = 0.523\,[rad]; \, \alpha_g = 0.191986\,[rad] \, \rho = 2.5 \times 10^{3}\,[\frac{kg}{m^3}], \, \gamma = 7.2 \times 10^{-1}\,[\frac{N}{m}], \, g = 9.81\,[\frac{m}{s^2}]\).

Computation shows that for the considered numerical data the limits of pressure differences are:

\[\label{eq3.7} L_i^{left} = -3591.47601 [Pa] \quad \text{and} \quad L_i^{right} = -847.5686305 [Pa], \tag{19}\] \[\label{eq3.8} L_e^{left} = -3483.843734 [Pa] \quad \text{and} \quad L_e^{right} = -617.6517706 [Pa]. \tag{20}\]

Therefore inequalities (13) and (14) becomes:

\[\label{eq3.9} -3591.47601 [Pa] \le p_i \le -847.5686305 [Pa], \tag{21}\] and \[\label{eq3.10} -3483.843734 [Pa] \le p_e \le -617.6517706 [Pa], \tag{22}\] respectively.

In the following we will illustrate first the theoretical (computational) existence/ nonexistence of static meniscus in case of Si tube having convex inner and outer surfaces.

The meridian curve of the inner free surface of convex meniscus can be obtained by solving the following initial value problem \[\label{eq3.11} \frac{dz_i}{dr} = \tan \alpha_i, \, \frac{d\alpha_i}{dr} = \frac{\rho g z_i – p_i}{\gamma} \times \tan \alpha_i – \frac{1}{r} \times \tan \alpha_i, \, z_i(0.0042) = 0, \, \alpha_i(0.0042) = 0.523, \tag{23}\] for different values of \(p_i \in [-3591.47601, 847.5686305]\, [Pa]\).

The meridian curve of the outer free surface of convex meniscus can be obtained by solving the following initial value problem \[\label{eq3.12} \frac{dz_e}{dr} = -\tan \alpha_e, \, \frac{d\alpha_e}{dr} = \frac{p_e – \rho g z_e}{\gamma} \times \frac{1}{\cos \alpha_e} \times \tan \alpha_e, \, z_e(0.0048) = 0, \quad \alpha_e(0.0048) = 0.523, \tag{24}\] for different values of \(p_e \in [-3483.843734,\,-617.6517706]\,[\text{Pa}]\).

In this way by computation the inner and outer surfaces meridian curves of a convex static Si meniscus is obtained for \(p_i = -2370\,[\text{Pa}]\) and \(p_e = -1650\,[\text{Pa}]\) respectively. The meridian curves \(z_i(r)\) and \(z_e(r)\) with the variation of the angles \(\alpha_i,\; \alpha_e\) are represented in Figures 11-14.

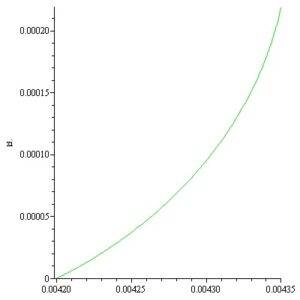
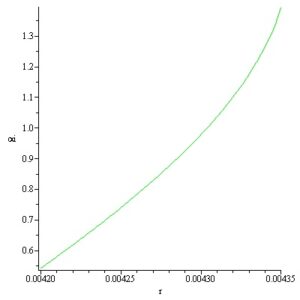
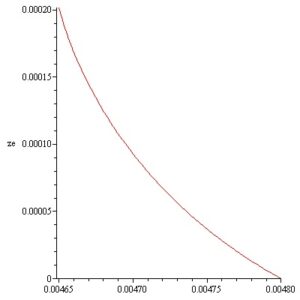
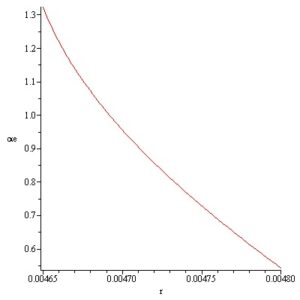
The static stability of the inner and outer free surfaces of an existing convex static meniscus it should be distinguished from the dynamic stability of the crystallization process considered in [17]–[21].

For statically stable convex meniscus, indispensable (necessary) first order conditions and also second order sufficient conditions for the minimum of functional (6) and (7) should be satisfied.

The first order necessary conditions are the Euler equations which leads to the Young-Laplace capillarity Eqs. (4) and (5).

The second order sufficient conditions for the minimum of functional (6) and (7) are the Legendre condition and the Jacobi condition [22].

The Legendre condition for the inner and outer surfaces are:

\[\label{eq3.13} \frac{\partial^2 F_i}{\partial z_i'^2} > 0, \quad \text{and} \quad \frac{\partial^2 F_e}{\partial z_e'^2} > 0, \tag{25}\] respectively.

Computing \(\dfrac{\partial^2 F_i}{\partial z_i' \partial z_i'}\) and \(\dfrac{\partial^2 F_e}{\partial z_e' \partial z_e'}\) we find

\[\frac{\partial^2 F_i}{\partial z_i' \partial z_i'} = \frac{r X Y}{(1 + (z_i')^2)^{3/2}} > 0, \quad \text{and} \quad \frac{\partial^2 F_e}{\partial z_e' \partial z_e'} = \frac{r X Y}{(1 + (z_e')^2)^{3/2}} > 0 ,\] respectively.

Therefore, the Legendre conditions are verified for the inner and outer free surfaces. The Jacoby condition concern the so-called Jacoby equation:

\[\label{eq3.14} \left[ \frac{\partial^2 F}{\partial z' \partial z'} – \frac{d}{dr} \left( \frac{\partial^2 F}{\partial z' \partial z'} \right) \right] \times \eta – \frac{d}{dr} \left[ \frac{\partial^2 F}{\partial z' \partial z'} \times \eta' \right] = 0. \tag{26}\]

In case of the functional (6) and (7).

Eq. (26) become:

\[\label{eq3.15} \frac{d}{dr} \left[ \frac{r X Y}{(1 + (z_i')^2)^{3/2}} \eta_i' \right] – g \times \rho \times r \times \eta_i = 0, \tag{27}\] and \[\label{eq3.16} \frac{d}{dr} \left[ \frac{r X Y}{(1 + (z_e')^2)^{3/2}} \eta_e' \right] – g \times \rho \times r \times \eta_e = 0, \tag{28}\] respectively.

Jacobi requirement of stability condition is that the solution of Eqs. (27) and (28) which verifies the initial condition \(\eta_i(R_{gi}) = 0\) and \(\eta_i'(R_{gi}) = 1\) vanishes at most ones on the interval \([R_{gi}, r_i]\) and \(\eta_e(r_e) = 0\), \(\eta_e'(r_e) = 1\) vanishes at most ones on the interval \([r_e, R_{ge}]\) respectively.

According to [22] for that it is sufficient to find Sturm type upper bounds for Eqs. (27) and (28).

Remark that for the coefficients of (27) and (28) the following inequalities hold:

\[\label{eq3.17} \frac{r X Y}{(1 + (z_i')^2)^{3/2}} > R_{gi} \times X \times (\sin \alpha_g)^3, \quad \text{and} \quad -g \times \rho \times r < -g \times \rho \times R_{gi}, \tag{29}\] and

\[\label{eq3.18} \frac{r X Y}{(1 + (z_e')^2)^{3/2}} > R_{ge} \times X \times (\cos \alpha_c)^3, \quad \text{and} \quad -g \times \rho \times r < -g \times \rho \times r_e, \tag{30}\] respectively.

Hence

\[\label{eq3.19} (\theta_i' \times R_{gi} \times X \times (\sin \alpha_g)^3)' – g \times \rho \times X \times R_{gi} = 0 \quad \text{or} \quad \theta_i'' = \frac{g \times \rho}{\gamma X (\sin \alpha_g)^3}, \tag{31}\] is a Sturm-type upper bound for (27). \[\label{eq3.20} (\theta_e' \times r_e \times X \times (\cos \alpha_c)^3)' – g \times \rho \times X \times r_e = 0, \quad \text{or} \quad \theta_e'' = \frac{g \times \rho}{\gamma X (\cos \alpha_c)^3}, \tag{32}\] is a Sturm–type upper bound for (28).

An arbitrary solution of (31) is given by \[\label{eq3.21} \theta_i(r) = A_i \times \sin(\omega_i \times r + \varphi_i), \tag{33}\] where \(A_i\) and \(\varphi_i\) are real constants and \[\label{eq3.22} \omega_i^2 = \frac{g \times \rho}{\gamma X (\sin \alpha_g)^3}, \tag{34}\] and an arbitrary solution of (32) is given by

\[\label{eq3.23} \theta_e(r) = A_e \times \sin(\omega_e \times r + \varphi_e), \tag{35}\] where \(A_e\) and \(\varphi_e\) are real constants and \[\label{eq3.24} \omega_e^2 = \frac{g \times \rho}{\gamma X (\cos \alpha_c)^3}. \tag{36}\]

The half period of a non-zero solution \(\theta_i(r)\), defined by (33), is given by \[\label{eq3.25} \frac{\pi}{\omega_i} = \pi \times \sqrt{\frac{\gamma X (\sin \alpha_g)^3}{g \times \rho}}. \tag{37}\]

If the half period given by (37) verifies inequality \[\label{eq3.26} r_i – R_{gi} < \pi \times \sqrt{\frac{\gamma X (\sin \alpha_g)^3}{g \times \rho}}, \tag{38}\] then the function \(\theta_i(r)\) defined by (33) vanishes at most ones on the interval \([R_{gi}, r_i]\)

Hence, according to [10] the solution of Jacobi Eq. (27) which verifies \(\eta_i(R_{gi}) = 0\) and \(\eta_i'(R_{gi}) = 1\) has at most one zero on the interval \([R_{gi}, r_i]\). Therefore, the stability condition of Jacobi is verified for the inner free surface.

The half period of a non-zero solution \(\theta_e(r)\), defined by (35), is given by

\[\label{eq3.27} \frac{\pi}{\omega_e} = \pi \times \sqrt{\frac{\gamma X (\cos \alpha_c)^3}{g \times \rho}}. \tag{39}\]

If the half period given by (39) verifies inequality

\[\label{eq3.28} R_{ge} – r_e < \pi \times \sqrt{\frac{\gamma X (\cos \alpha_c)^3}{g \times \rho}}, \tag{40}\] then the function \(\theta_e(r)\) defined by (35) vanishes at most ones on the interval \([r_e, R_{ge}]\)

Hence, according to [10] the solution of Jacobi Eq. (28) which verifies \(\eta_e(r_e)=0\) and \(\eta_e'(r_e)=1\) has at most one zero on the interval \([r_e, R_{ge}]\). Therefore, the stability condition of Jacobi is verified for the outer free surface.

In case of convex tube, the static stability of the inner and outer free surfaces is:

\[\label{eq3.29} r_i – R_{gi} < \pi \times \sqrt{\frac{\gamma X (\sin \alpha_g)^3}{g \times \rho}} , \quad \text{and} \quad R_{ge} – r_e < \pi \times \sqrt{\frac{\gamma X (\cos \alpha_c)^3}{g \times \rho}}. \tag{41}\]

Inequalities (41) represent a sufficient condition of stability for a static convex meniscus which exist theoretically for a certain value of the pressure differences \(p_i, p_e\). Note that inequalities (41) is not a necessary condition of stability i.e. violation of one or both inequalities not imply instability.

For find sufficient condition concerning instability the Jacobi requirement of instability condition has to be proven. This condition for the inner surface is: solution of Eq. (27) which verifies the initial condition \(\eta_i(R_{gi})=0\) and \(\eta_i'(R_{gi})=1\) vanishes at least twice on the interval \([R_{gi}, r_i]\). For the outer surface is: solution of Eq. (28) which verifies the initial condition \(\eta_e(r_e)=0\), \(\eta_e'(r_e)=1\) vanishes at least twice on the interval \([r_e, R_{ge}]\).

According to [22] for that it is sufficient to find Sturm type lower bounds for Eqs. (27) and (28).

Remark that for the coefficients of (27) and (28) the following inequalities hold:

\[\label{eq3.30} \frac{r X Y}{(1+(z_i')^2)^{3/2}} < R_{gi} \times X \times (\cos \alpha_c)^3, \quad \text{and} \quad -g \times \rho \times r > -g \times \rho \times r_i, \tag{42}\] and \[\label{eq3.31} \frac{r X Y}{(1+(z_e')^2)^{3/2}} < R_{ge} \times X \times (\sin \alpha_g)^3, \quad \text{and} \quad -g \times \rho \times r < -g \times \rho \times R_{ge}, \tag{43}\] respectively.

Hence \[\label{eq3.32} (\theta_i' \times r_i \times X \times (\cos \alpha_c)^3)' – g \times \rho \times X \times r_i = 0, \quad \text{or} \quad \theta_i'' = \frac{g \times \rho}{\gamma X (\cos \alpha_c)^3}, \tag{44}\] is a Sturm–type lower bound for (27), and \[\label{eq3.33} (\theta_e' \times R_{ge} \times X \times (\sin \alpha_g)^3)' – g \times \rho \times X \times R_{ge} = 0, \quad \text{or} \quad \theta_e'' = \frac{g \times \rho}{\gamma X (\sin \alpha_g)^3}, \tag{45}\] is a Sturm–type lower bound for (28).

An arbitrary solution of (44) is given by

\[\label{eq3.34} \theta_i(r) = A_i \times \sin(\omega_i \times r + \varphi_i), \tag{46}\] where \(A_i\) and \(\varphi_i\) are real constants and

\[\label{eq3.35} \omega_i^2 = \frac{g \times \rho}{\gamma X (\cos \alpha_c)^3}, \tag{47}\] and an arbitrary solution of (45) is given by

\[\label{eq3.36} \theta_e(r) = A_e \times \sin(\omega_e \times r + \varphi_e), \tag{48}\] where \(A_e\) and \(\varphi_e\) are real constants and

\[\label{eq3.37} \omega_e^2 = \frac{g \times \rho}{\gamma X (\sin \alpha_g)^3}. \tag{49}\]

The period of a non-zero solution \(\theta_i(r)\), defined by (33), is given by

\[\label{eq3.38} \frac{2 \pi}{\omega_i} = 2 \times \pi \times \sqrt{\frac{\gamma X (\cos \alpha_c)^3}{g \times \rho}}. \tag{50}\]

If the half period given by (50) verifies inequality \[\label{eq3.39} \frac{2 \pi}{\omega_i} = 2 \times \pi \times \sqrt{\frac{\gamma X (\cos \alpha_c)^3}{g \times \rho}} < r_i – R_{gi}, \tag{51}\] then the function \(\theta_i(r)\) defined by (46) vanishes at least twice on the interval \([R_{gi}, r_i]\).

Hence, according to [10] the solution of Jacobi Eq. (27) which verifies \(\eta_i(R_{gi}) = 0\) and \(\eta_i'(R_{gi}) = 1\) has at least two zero on the interval \([R_{gi}, r_i]\). Therefore, the instability condition of Jacobi is verified for the inner free surface.

The period of a non-zero solution \(\theta_e(r)\), defined by (48), is given by, \[\label{eq3.40} \frac{2 \pi}{\omega_e} = 2 \times \pi \times \sqrt{\frac{\gamma X (\sin \alpha_g)^3}{g \times \rho}}. \tag{52}\]

If the period given by (52) verifies inequality

\[\label{eq3.41} \frac{2 \pi}{\omega_e} = 2 \times \pi \times \sqrt{\frac{\gamma X (\sin \alpha_g)^3}{g \times \rho}} < R_{ge} – r_e, \tag{53}\] then the function \(\theta_e(r)\) defined by (48) vanishes at least twice on the interval \([r_e, R_{ge}]\)

Hence, according to [10] the solution of Jacobi Eq. (28) which verifies \(\eta_e(r_e) = 0\) and \(\eta_e'(r_e) = 1\) has at least two zero on the interval \([r_e, R_{ge}]\). Therefore, the instability condition of Jacobi is verified for the outer free surface.

In case of convex meniscus, the static instability conditions of the inner and outer free surfaces are: \[\label{eq3.42} 2 \times \pi \times \sqrt{\frac{\gamma X (\cos \alpha_c)^3}{g \times \rho}} < r_i – R_{gi} , \quad \text{and} \quad 2 \times \pi \times \sqrt{\frac{\gamma X (\sin \alpha_g)^3}{g \times \rho}} < R_{ge} – r_e. \tag{54}\]

Inequalities (54) rep resent a sufficient condition of instability for a static convex meniscus which exist theoretically for a certain value of the pressure differences \(p_i, p_e\). Note that inequalities (54) are not a necessary conditions of instability i.e. violation of one or both inequalities not imply stability.

For the considered Si tube the sufficient conditions of stability of the inner and outer surfaces are:

\[\label{eq3.43} 0.00015 = r_i – R_{gi} < \pi \times \sqrt{\frac{\gamma X (\sin \alpha_g)^3}{g \times \rho}} = 0.001418760703, \tag{55}\] \[\label{eq3.44} 0.00015 = R_{ge} – r_e < \pi \times \sqrt{\frac{\gamma X (\cos \alpha_c)^3}{g \times \rho}} = 0.01372564021. \tag{56}\]

Since inequalities (55) and (56), are valid the inner and outer surfaces of the static convex Si meniscus are stables.

The sufficient condition of instability of the inner and outer surfaces are:

\[\label{eq3.45} 0.00015 = r_i – R_{gi} > 2 \times \pi \times \sqrt{\frac{\gamma X (\cos \alpha_c)^3}{g \times \rho}} = 0.02745128041, \tag{57}\]

\[\label{eq3.46} 0.00015 = R_{ge} – r_e > 2 \times \pi \times \sqrt{\frac{\gamma X (\sin \alpha_g)^3}{g \times \rho}} = 0.002837521406. \tag{58}\]

Since inequalities (57) and (58), are false for the inner and outer surfaces of the static convex Si meniscus the instability criteria (54) cannot be applied.

4. Existence, Stability or Instability of a meniscus having concave inner and outer free surface

The inner and outer free surface of a meniscus is concave if \(z_i''(r) < 0\) and \(z_e''(r) < 0\) for \(R_{gi} \le r \le r_i\) and \(r_e < r < R_{ge}\) respectively.

Remark first that in case of a meniscus having concave inner and outer surfaces the functions \(z_i'(r)\), \(z_e'(r)\) are decreasing. For the inner meridian curve this means that the angle between the tangent line to the meridian curve \(z_i(r)\), in every point \(r\), and the \(Or\) axis, \(\alpha_i(r) = \arctan z_i'(r)\), is decreasing. In particular, it follows that \(\alpha_i(R_{gi}) > \alpha_i(r_i)\). Since \(\alpha_i(R_{gi}) = \alpha_c\) and \(\alpha_i(r_i) = \frac{\pi}{2} – \alpha_g\), we obtain inequality \(\frac{\pi}{2} – \alpha_g < \alpha_c\), or \(\alpha_g < \alpha_c > 0\). (see Figure 10). For the outer surface meridian curve convexity means that the angle between the tangent line to the meridian curve \(z_e(r)\), in every point \(r\), and the \(Or\) axis, \(\alpha_e(r) = -\arctan z_e'(r)\), is increasing. In particular, it follows that \(\alpha_e(R_{ge}) > \alpha_e(r_e)\). Since \(\alpha_e(R_{ge}) = \alpha_c\) and \(\alpha_e(r_e) = \frac{\pi}{2} – \alpha_g\) we obtain inequality \(\frac{\pi}{2} – \alpha_g < \alpha_c > 0\) (see Figure 10). Therefore if the inner and outer free surface of a meniscus is concave then \[\frac{\pi}{2} – \alpha_g < \alpha_c.\]

Using the Young-Laplace capillarity Eqs. (4) and (5) and conditions (11) and (12) respectively in [20] the following result was established:

If \(p_i\) and \(p_e\) there exists a solution \(z_i(r)\) of Eq. (4) and a solution \(z_e(r)\) of Eq. (5) respectively, which are concave meridian curves and describes the inner and outer free surfaces of a static meniscus respectively, then the following inequalities hold:

\[\begin{aligned} \label{eq4.1} \gamma &\frac{(a_c + a_g)}{r_i – R_{gi}} \frac{\pi}{2} \cos \alpha_c – \frac{Y}{R_{gi}} \sin \alpha_c \notag\\ &\le p_i \le \gamma \frac{(a_c + a_g)}{r_i – R_{gi}} \frac{\pi}{2} \sin \alpha_g + (r_i – R_{gi}) \rho g \tan(\alpha_c) – \frac{Y}{r_i} \cos \alpha_g, \end{aligned} \tag{59}\]

\[\begin{aligned} \label{eq4.2} \gamma &\frac{(a_c + a_g)}{R_{ge} – r_e} \frac{\pi}{2} \cos \alpha_c + \frac{Y}{R_{ge}} \cos \alpha_g \notag\\&\le p_e \le \gamma \frac{(a_c + a_g)}{R_{ge} – r_e} \frac{\pi}{2} \sin \alpha_g + (R_{ge} – r_e) \rho g \tan(\alpha_c) + \frac{Y}{R_{ge}} \sin \alpha_c. \end{aligned} \tag{60}\]

Therefore in case of the existence of a computed static meniscus for which the inner and outer surfaces are concave then the values of the pressure differences \(p_i = -p_{gi} – \rho \times g \times H\) and \(p_e = -p_{ge} – \rho \times g \times H\) has to be in the interval \(\left[L_i^{left}, L_i^{right}\right]\) and \(\left[L_e^{left}, L_e^{right}\right]\) respectively where:

\[ L_i^{left} = \gamma \frac{(a_c + a_g)}{r_i – R_{gi}} \frac{\pi}{2} \cos \alpha_c – \frac{Y}{R_{gi}} \sin \alpha_c,\label{eq4.3}\ \tag{61}\] \[L_i^{right} = \gamma \frac{(a_c + a_g)}{r_i – R_{gi}} \frac{\pi}{2} \sin \alpha_g + (r_i – R_{gi}) \rho g \tan(\alpha_c) – \frac{Y}{r_i} \cos \alpha_g, \tag{62}\] \[L_e^{left} = \gamma \frac{(a_c + a_g)}{R_{ge} – r_e} \frac{\pi}{2} \cos \alpha_c + \frac{Y}{R_{ge}} \cos \alpha_g, \ \tag{63}\] \[ L_e^{right} = \gamma \frac{(a_c + a_g)}{R_{ge} – r_e} \frac{\pi}{2} \sin \alpha_g + (R_{ge} – r_e) \rho g \tan(\alpha_c) + \frac{Y}{R_{ge}} \sin \alpha_c.\label{eq4.6} \tag{64}\]

For the practical existence of a static meniscus having the inner and outer free surfaces concave numerical computations were performed for InSb thin tube growth using the following numerical data: \(R_{gi} = 4.2 \times 10^{-3}\,[\text{m}],\; r_i = 4.35 \times 10^{-3}\,[\text{m}],\; R_{ge} = 4.8 \times 10^{-3}\,[\text{m}],\; r_e = 4.65 \times 10^{-3}\,[\text{m}]\) \(\alpha_c = 1.1128955\,[\text{rad}],\; \alpha_g = 0.541444\,[\text{rad}],\; \rho = 6.582 \times 10^3\,[\frac{\text{kg}}{\text{m}^3}],\; \gamma = 4.2 \times 10^{-1}\,[\frac{\text{N}}{\text{m}}],\; g = 9.81\,[\frac{\text{m}}{\text{s}^2}]\)

Computation shows that for the considered numerical data, the inequality (59) becomes:

\[\label{eq4.7} 13.763836\,[\text{Pa}] \le p_i \le 52.082108\,[\text{Pa}], \tag{65}\] \[\label{eq4.8} L_i^{left} = 13.763836\, [\text{Pa}], \quad \text{and} \quad L_i^{right} = 52.082108\, [\text{Pa}], \tag{66}\] and inequality (60) becomes

\[\label{eq4.9} 178.449362\, [\text{Pa}] \le p_e \le 221.431533\, [\text{Pa}], \tag{67}\] \[\label{eq4.10} L_e^{left} = 178.449362\, [\text{Pa}], \quad \text{and} \quad L_e^{right} = 221.431533\, [\text{Pa}]. \tag{68}\]

In the following we will illustrate first the existence of concave inner and outer free surfaces in case of a static InSb meniscus.

The meridian curve of the outer free surface of concave meniscus can be obtained by solving the following initial value problem

\[\label{eq4.11} \frac{dz_i}{dr} = \tan \alpha_i, \, \frac{d\alpha_i}{dr} = \frac{\rho g z_i – p_i}{\gamma} \frac{1}{\cos \alpha_i} – \frac{1}{r} \tan \alpha_i, \, z_i(0.0042) = 0,\, \alpha_i(0.0042) = 1.112955, \tag{69}\] for different values of \(p_i \in [13.763836, 52.082108]\, [\text{Pa}]\).

The meridian curve of the outer free surface of concave meniscus can be obtained by solving the following initial value problem

\[\label{eq4.12} \frac{dz_e}{dr} = -\tan \alpha_e, \, \frac{d\alpha_e}{dr} = \frac{p_e – \rho g z_e}{\gamma} \frac{1}{\cos \alpha_e} – \frac{1}{r} \tan \alpha_e, \, z_e(0.0048) = 0, \, \alpha_e(0.0048) = 1.112955, \tag{70}\] for different values of \(p_e \in [178.449362, 221.431533]\, [\text{Pa}]\).

In this way by computation the inner and outer surfaces meridian curves of a convex static Si meniscus is obtained for \(p_i = 35\,[\text{Pa}]\) and \(p_e = [\text{Pa}]\) respectively. The meridian curves \(z_i(r)\) and \(z_e(r)\) with the variation of the angles \(\alpha_i, \alpha_e\) are represented on the next Figures 15-18:

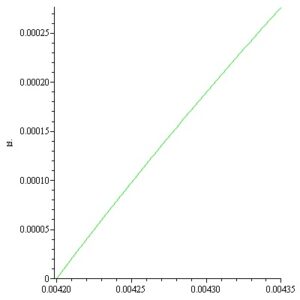
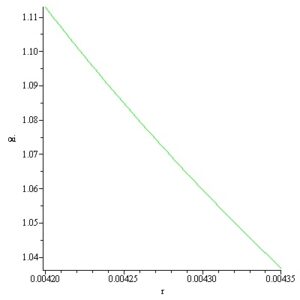
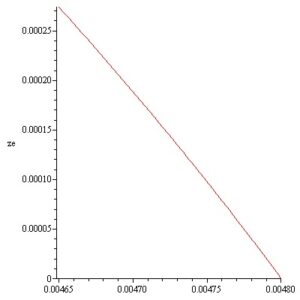
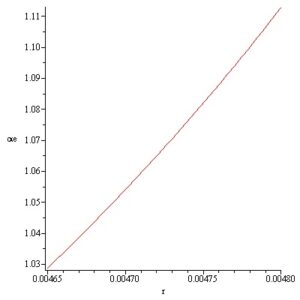
The static stability of the inner and outer free surfaces of an existing convex static meniscus it should be distinguished from the dynamic stability of the crystallization process considered in [17]–[21].

For statically stable convex meniscus, indispensable (necessary) first order conditions and also second order sufficient conditions for the minimum of functional (6) and (7) should be satisfied.

The first order necessary conditions are the Euler equations which leads to the Young-Laplace capillary Eqs. (4) and (5).

The second order sufficient conditions for the minimum of functional (6) and (7) are the Legendre condition and the Jacobi condition [22].

The Legendre condition for the inner and outer surfaces are: \[\label{eq4.13} \frac{\partial^2 F_i}{\partial z_i'^2} > 0 \quad \text{and} \quad \frac{\partial^2 F_e}{\partial z_e'^2} > 0, \tag{71}\] respectively.

Computing \(\dfrac{\partial^2 F_i}{\partial z_i'^2}\) and \(\dfrac{\partial^2 F_e}{\partial z_e'^2}\) we find \[\frac{\partial^2 F_i}{\partial z_i'^2} = \frac{r X Y}{(1 + (z_i')^2)^{3/2}} > 0 \quad \text{and} \quad \frac{\partial^2 F_e}{\partial z_e'^2} = \frac{r X Y}{(1 + (z_e')^2)^{3/2}} > 0 ,\] respectively.

Therefore, the Legendre conditions are verified for the inner and outer free surfaces.

The Jacoby condition concern the so-called Jacoby equation:

\[\label{eq4.14} \left[ \frac{\partial^2 F}{\partial z'^2} – \frac{d}{dr} \left( \frac{\partial^2 F}{\partial z'^2} \right) \right] \times \eta – \frac{d}{dr} \left[ \frac{\partial^2 F}{\partial z'^2} \times \eta' \right] = 0. \tag{72}\]

In case of the functional (6) and (7), Eq. (72) becomes:

\[\label{eq4.15} \frac{d}{dr} \left[ \frac{r X Y}{(1 + (z_i')^2)^{3/2}} \eta_i' \right] – g \times \rho \times r \times \eta_i = 0, \tag{73}\] \[\label{eq4.16} \frac{d}{dr} \left[ \frac{r X Y}{(1 + (z_e')^2)^{3/2}} \eta_e' \right] – g \times \rho \times r \times \eta_e = 0, \tag{74}\] respectively.

Jacobi requirement of stability condition is that the solution of Eqs. (73) and (74) which verifies the initial condition \(\eta_i(R_{gi}) = 0\) and \(\eta_i'(R_{gi}) = 1\) vanishes at most ones on the interval \([R_{gi}, r_i]\) and \(\eta_e(r_e) = 0\), \(\eta_e'(r_e) = 1\) vanishes at most ones on the interval \([r_e, R_{ge}]\) respectively.

According to [22] for that it is sufficient to find Sturm type upper bounds for Eqs. (73) and (74).

Remark that for the coefficients of (73) and (74) the following inequalities hold:

\[\label{eq4.17} \frac{r X Y}{(1 + (z_i')^2)^{3/2}} > R_{gi} \times X \times (\sin \alpha_g)^3 , \quad \text{and} \quad – g \times \rho \times r < – g \times \rho \times R_{gi}, \tag{75}\] \[\label{eq4.18} \frac{r X Y}{(1 + (z_e')^2)^{3/2}} > r_e \times X \times (\cos \alpha_c)^3 , \quad \text{and} \quad – g \times \rho \times r < – g \times \rho \times r_e, \tag{76}\] respectively.

Hence, \[\label{eq4.19} \left( \theta_i' \times R_{gi} \times X \times (\sin \alpha_g)^3 \right)' – g \times \rho \times X \times R_{gi} = 0, \quad \text{or} \quad \theta_i'' = \frac{g \times \rho}{\gamma X (\sin \alpha_g)^3}, \tag{77}\] is a Sturm–type upper bound for (73), and \[\label{eq4.20} \left( \theta_e' \times r_e \times X \times (\cos \alpha_c)^3 \right)' – g \times \rho \times X \times r_e = 0, \quad \text{or} \quad \theta_e'' = \frac{g \times \rho}{\gamma X (\cos \alpha_c)^3}, \tag{78}\] is a Sturm–type upper bound for (74). An arbitrary solution of (77) is given by \[\label{eq4.21} \theta_i(r) = A_i \times \sin(\omega_i \times r + \varphi_i), \tag{79}\] where \(A_i\) and \(\varphi_i\) are real constants and \[\label{eq4.22} \omega_i^2 = \frac{g \times \rho}{\gamma X (\sin \alpha_g)^3}, \tag{80}\] and an arbitrary solution of (78) is given by \[\label{eq4.23} \theta_e(r) = A_e \times \sin(\omega_e \times r + \varphi_e), \tag{81}\] where \(A_e\) and \(\varphi_e\) are real constants and \[\label{eq4.24} \omega_e^2 = \frac{g \times \rho}{\gamma X (\cos \alpha_c)^3}. \tag{82}\]

The half period of a non-zero solution \(\theta_i(r)\), defined by (79), is given by

\[\label{eq4.25} \frac{\pi}{\omega_i} = \pi \times \sqrt{\frac{\gamma X (\sin \alpha_g)^3}{g \times \rho}}. \tag{83}\]

If the half period given by (83) verifies inequality

\[\label{eq4.26} r_i – R_{gi} < \pi \times \sqrt{\frac{\gamma X (\sin \alpha_g)^3}{g \times \rho}}, \tag{84}\] then the function \(\theta_i(r)\) defined by (79) vanishes at most ones on the interval \([R_{gi}, r_i]\).

Hence, according to [10] the solution of Jacobi equation (73) which verifies \(\eta_i(R_{gi}) = 0\) and \(\eta_i'(R_{gi}) = 1\) has at most one zero on the interval \([R_{gi}, r_i]\). Therefore, the stability condition of Jacobi is verified for the inner free surface.

The half period of a non-zero solution \(\theta_e(r)\), defined by (81), is given by

\[\label{eq4.27} \frac{\pi}{\omega_e} = \pi \times \sqrt{\frac{\gamma X (\cos \alpha_c)^3}{g \times \rho}}. \tag{85}\]

If the half period given by (85) verifies inequality

\[\label{eq4.28} R_{ge} – r_e < \pi \times \sqrt{\frac{\gamma X (\cos \alpha_c)^3}{g \times \rho}}, \tag{86}\] then the function \(\theta_e(r)\) defined by (81) vanishes at most ones on the interval \([r_e, R_{ge}]\).

Hence, according to [10] the solution of Jacobi Eq. (74) which verifies \(\eta_e(r_e) = 0\) and \(\eta_e'(r_e) = 1\) has at most one zero on the interval \([r_e, R_{ge}]\). Therefore, the stability condition of Jacobi is verified for the outer free surface.

In case of concave tube, the static stability of the inner and outer free surfaces is:

\[\label{eq4.29} r_i – R_{gi} < \pi \times \sqrt{\frac{\gamma X (\sin \alpha_g)^3}{g \times \rho}} , \quad \text{and} \quad R_{ge} – r_e < \pi \times \sqrt{\frac{\gamma X (\cos \alpha_c)^3}{g \times \rho}}. \tag{87}\]

Inequalities (87) represent a sufficient condition of stability for a static convex meniscus which exist theoretically for a certain value of the pressure differences \(p_i,\; p_e\). Note that inequalities (87) is not a necessary condition of stability i.e. violation of one or both inequalities not imply instability.

For find sufficient condition concerning instability the Jacobi requirement of instability condition has to be proven. This condition for the inner surface is: solution of (73) which verifies the initial condition \(\eta_i(R_{gi}) = 0\) and \(\eta_i'(R_{gi}) = 1\) vanishes at least twice on the interval \([R_{gi}, r_i]\). For the outer surface is: solution of (74) which verifies the initial condition \(\eta_e(r_e) = 0\), \(\eta_e'(r_e) = 1\) vanishes at least twice on the interval \([r_e, R_{ge}]\).

According to [22] for that it is sufficient to find Sturm type lower bounds for Eqs. (73) and (74).

Remark that for the coefficients of (73) and (74) the following inequalities hold: \[\label{eq4.30} \frac{r X Y}{(1 + (z_i')^2)^{3/2}} < r_i \times X \times (\cos \alpha_c)^3 , \quad \text{and} \quad – g \times \rho \times r > – g \times \rho \times r_i, \tag{88}\] \[\label{eq4.31} \frac{r X Y}{(1 + (z_e')^2)^{3/2}} < R_{ge} \times X \times (\sin \alpha_g)^3, \quad \text{and} \quad – g \times \rho \times r < – g \times \rho \times R_{ge}, \tag{89}\] respectively.

Hence \[\label{eq4.32} \left( \theta_i' \times r_i \times X \times (\cos \alpha_c)^3 \right)' – g \times \rho \times X \times r_i = 0 , \quad \text{or} \quad \theta_i'' = \frac{g \times \rho}{\gamma X (\cos \alpha_c)^3}, \tag{90}\] is a Sturm–type lower bound for (73), and \[\label{eq4.33} \left( \theta_e' \times R_{ge} \times X \times (\sin \alpha_g)^3 \right)' – g \times \rho \times X \times R_{ge} = 0 , \quad \text{or} \quad \theta_e'' = \frac{g \times \rho}{\gamma X (\sin \alpha_g)^3}, \tag{91}\] is a Sturm–type lower bound for (74). An arbitrary solution of (90) is given by \[\label{eq4.34} \theta_i(r) = A_i \times \sin(\omega_i \times r + \varphi_i), \tag{92}\] where \(A_i\) and \(\varphi_i\) are real constants and \[\label{eq4.35} \omega_i^2 = \frac{g \times \rho}{\gamma X (\cos \alpha_c)^3}, \tag{93}\] and an arbitrary solution of (91) is given by \[\label{eq4.36} \theta_e(r) = A_e \times \sin(\omega_e \times r + \varphi_e), \tag{94}\] where \(A_e\) and \(\varphi_e\) are real constants and

\[\label{eq4.37} \omega_e^2 = \frac{g \times \rho}{\gamma X (\sin \alpha_g)^3}. \tag{95}\]

The period of a non-zero solution \(\theta_i(r)\), defined by (79), is given by \[\label{eq4.38} \frac{2 \pi}{\omega_i} = 2 \times \pi \times \sqrt{\frac{\gamma X (\cos \alpha_c)^3}{g \times \rho}}. \tag{96}\]

If the half period given by (96) verifies inequality

\[\label{eq4.39} \frac{2 \pi}{\omega_i} = 2 \times \pi \times \sqrt{\frac{\gamma X (\cos \alpha_c)^3}{g \times \rho}} < r_i – R_{gi}, \tag{97}\] then the function \(\theta_i(r)\) defined by (92) vanishes at least twice on the interval \([R_{gi}, r_i]\)

Hence, according to [10] the solution of Jacobi equation (73) which verifies \(\eta_i(R_{gi}) = 0\) and \(\eta_i'(R_{gi}) = 1\) has at least two zeros on the interval \([R_{gi}, r_i]\). Therefore, the instability condition of Jacobi is verified for the inner free surface.

The period of a non-zero solution \(\theta_e(r)\), defined by (94), is given by

\[\label{eq4.40} \frac{2 \pi}{\omega_e} = 2 \times \pi \times \sqrt{\frac{\gamma X (\sin \alpha_g)^3}{g \times \rho}}. \tag{98}\]

If the period given by (98) verifies inequality

\[\label{eq4.41} \frac{2 \pi}{\omega_e} = 2 \times \pi \times \sqrt{\frac{\gamma X (\sin \alpha_g)^3}{g \times \rho}} < R_{ge} – r_e, \tag{99}\] then the function \(\theta_e(r)\) defined by (94) vanishes at least twice on the interval \([r_e, R_{ge}]\)

Hence, according to [10] the solution of Jacobi equation (74) which verifies \(\eta_e(r_e) = 0\) and \(\eta_e'(r_e) = 1\) has at least two zeros on the interval \([r_e, R_{ge}]\). Therefore, the instability condition of Jacobi is verified for the outer free surface.

In case of concave meniscus, the static instability conditions of the inner and outer free surfaces are:

\[\label{eq4.42} 2 \times \pi \times \sqrt{\frac{\gamma X (\cos \alpha_c)^3}{g \times \rho}} < r_i – R_{gi} \quad \text{and} \quad 2 \times \pi \times \sqrt{\frac{\gamma X (\sin \alpha_g)^3}{g \times \rho}} < R_{ge} – r_e. \tag{100}\]

Inequalities (100) represent a sufficient condition of instability for a static convex meniscus which exist theoretically for a certain value of the pressure differences \(p_i,\; p_e\). Note that inequalities (100) are not a necessary condition of instability i.e. violation of one or both inequalities not imply stability.

For the considered InSb tube the sufficient conditions of stability of the inner and outer surfaces are:

\[\label{eq4.43} 0.00015 = r_i – R_{gi} < \pi \times \sqrt{\frac{\gamma X (\sin \alpha_g)^3}{g \times \rho}} = 0.002964425109, \tag{101}\] \[\label{eq4.44} 0.00015 = R_{ge} – r_e < \pi \times \sqrt{\frac{\gamma X (\cos \alpha_c)^3}{g \times \rho}} = 0.002354579340. \tag{102}\]

Since inequalities (101) and (102), are valid the inner and outer surfaces of the static convex InSb meniscus are stables.

The sufficient condition of instability of the inner and outer surfaces are:

\[\label{eq4.45} 0.00015 = r_i – R_{gi} > 2 \times \pi \times \sqrt{\frac{\gamma X (\cos \alpha_c)^3}{g \times \rho}} = 0.00470958679, \tag{103}\] \[\label{eq4.46} 0.00015 = R_{ge} – r_e > 2 \times \pi \times \sqrt{\frac{\gamma X (\sin \alpha_g)^3}{g \times \rho}} = 0.005928850218. \tag{104}\]

Since inequalities (103) and (104), are false for the inner and outer surfaces of the static convex InSb meniscus the instability criteria (100) cannot be applied.

5. Results

Necessary conditions for the existence and sufficient conditions for the stability or instability of the static meniscus (liquid bridge) appearing in the thin tube single crystal growth from the melt, of predetermined sizes, by using the edge-defined-film- fed (EFG) growth method, are presented. Theoretical results are illustrated numerically in case of Si and InSb tube case single crystal growth by EFG method.

6. Comments and Conclusions

The main novelty in this article consists in the obtained inequalities. These represent limits for what can and cannot be achieved. Experimentally, only stable static liquid bridges can be created if they exist theoretically. Unstable static liquid bridges could exist just in theory; in reality, they collapse; therefore, they are not appropriate for crystal growth.

Authors Contribution

The authors contributed equally to the realization of this work. All authors have read and agreed to the published version of the manuscript. Founding. This research did not receive any specific grant from founding agencies in the public, commercial or not-for-profit sectors.

Data Availability Statement

The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.